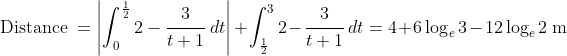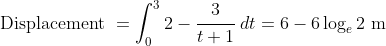The faster way is to consider the position of the particle at the start and finish of the period of interest,
plus at any times in the interval when it stops (hence part (c)) as it may change directions.
} \\ &= 2(0) - 3\log_e{(0+1)} \\ &= 0 - 3\log_e{1} \\ &= 0\ \text{m} \qquad \text{as $\log_e{1}=0$} \end{align*})
} \\ &= 2(3) - 3\log_e{(3+1)} \\ &= 6 - 3\log_e{4} \\ &= 6 - 6\log_e{2}\ \text{m} \qquad \text{as $\log_e{4} = \log_e{\left(2^2\right)}=2\log_e{2}$} \end{align*})
From part (c), we know that the particle is stationary at
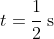
, so check
} \\ &= 2\left(\cfrac{1}{2}\right) - 3\log_e{\left(\cfrac{1}{2}+1\right)} \\ &= 1 - 3\log_e{\left(\cfrac{3}{2}\right)} \\ &= 1 - 3\log_e{3} + 3\log_e{2}\ \text{m} \qquad \text{as $\log_e{\left(\cfrac{3}{2}\right)} = \log_e{3} - \log_e{2}$} \end{align*})
So, the particle's travel path:
And so, over this period of 3 s,
\bigg] + \bigg[6 - 6\log_e{2} - \big(1 - 3\log_e{3} + 3\log_e{2}\big)\bigg] \\ &= -1 + 3\log_e{3} - 3\log_e{2} + 6 - 6\log_e{2} - 1 + 3\log_e{3} - 3\log_e{2} \\ &= \big(-1 + 6 - 1\big) + \big(3 + 3\big)\log_e{3} + \big(-3 - 6 - 3\big)\log_e{2} \\ &= 4 + 6\log_e{3} - 12\log_e{2}\ \text{m} \\ &\approx 2.2739...\ \text{m} \end{align*})
while its total displacement is
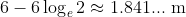
.
Using the integration approach, you should find: