Example: A square and a circle.
Let the string be divided into two pieces, one of length
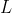
metres and the other of length
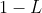
metres.
Take the first piece and make it into a circle. The circumference of the circle will be the length of the piece of string, so if the circle has radius of
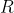
metres then we know that
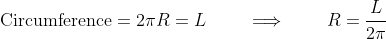
and so we can determine the area of the circle:
^2 = \cfrac{\pi L^2}{4\pi^2} = \cfrac{L^2}{4\pi})
Now, take the second piece and make it into a square. The square will have sides of length
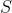
metres and its perimeter will be the same as the length of the piece of string used to make it:

and so we can determine the area of the square:
^2 = \cfrac{(1 - L)^2}{16})
We can now determine what length to make the two pieces by making the two areas equal:
^2}{16} \\ \cfrac{L^2}{(1 - L)^2} &= \cfrac{4\pi}{16} \\ \left(\cfrac{L}{1 - L}\right)^2 &= \cfrac{\pi}{4} \\ \cfrac{L}{1 - L} &= \sqrt{\cfrac{\pi}{4}} \qquad \text{as $L$ and $1 - L$ must both be positive} \\ &= \cfrac{\sqrt{\pi}}{2} \\ 2L &= \sqrt{\pi}(1 - L) \\ &= \sqrt{\pi} - L\sqrt{\pi} \\ 2L + L\sqrt{\pi} &= \sqrt{\pi} \\ L\left(2 + \sqrt{\pi}\right) &= \sqrt{\pi} \\ L &= \cfrac{\sqrt{\pi}}{2 + \sqrt{\pi}} \\ &= \cfrac{\sqrt{\pi}}{2 + \sqrt{\pi}} \times \cfrac{2 - \sqrt{\pi}}{2 - \sqrt{\pi}} \\ &= \cfrac{\sqrt{\pi}\left(2 - \sqrt{\pi}\right)}{2^2 - \left(\sqrt{\pi}\right)^2} \\ &= \cfrac{2\sqrt{\pi} - \left(\sqrt{\pi}\right)^2}{4 - \pi} \\ &= \cfrac{2\sqrt{\pi} - \pi}{4 - \pi} \\ &\approx 0.46984...\ \text{m} \end{align*})
So, if I use
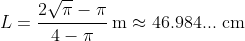
of the string to make a circle with radius
}\ \text{m} \approx 7.4777...\ \text{cm})
and hence with area
}{4\pi^2(4 - \pi)^2}\ \text{m}^2 = \cfrac{2500\left(2 - \sqrt{\pi}\right)^2}{(4 - \pi)^2}\ \text{cm}^2 \approx 175.667...\ \text{cm}^2)
then I can use the other
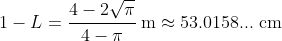
of the string to make a square of side length
}\ \text{m} \approx 13.2539...\ \text{cm})
and hence of area
^2}{4(4 - \pi)^2}\ \text{m}^2 = \cfrac{2500\left(2 - \sqrt{\pi}\right)^2}{(4 - \pi)^2}\ \text{cm}^2 \approx 175.667...\ \text{cm}^2)
.
Note that, as required, the two areas are identical, both being
^2}{(4 - \pi)^2}\ \text{cm}^2.)
This is one example. I think you will find that making a square and an equilateral triangle, or a 2:1 rectangle and a square, or some other combination along these lines, will turn out to have nicer algebra than this solution using a circle.