frenzal_dude
UTS Student
I need to find the absolute value of b(t):
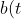=a(t)[1+e^{-j2\pi tT}])
Here is the answer in the textbook:
 \right |=\left | a(t) \right |\sqrt{2(1+cos(2\pi tT)}2|cos(\pi tT)|)
However I got a different answer when working it out, and can't understand how they got to that result from the textbook.
Here is my working out:
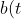=a(t)+a(t)cos(2\pi tT)-a(t)jsin(2\pi tT))
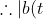|=\sqrt{[a(t)+a(t)cos(2\pi tT)]^{2}+[a(t)sin(2\pi tT)]^{2}})
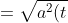+2a(t)cos(2\pi tT)+a^{2}(t)cos^{2}(2\pi tT)+a^{2}(t)sin^{2}(2\pi tT)})
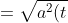[1+2\sqrt{a(t)}cos(2\pi tT) + cos^{2}(2\pi tT)+sin^{2}(2\pi tT)]})
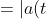|\sqrt{2+2\sqrt{a(t)}cos(2\pi tT)})
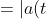|\sqrt{2[1+\sqrt{a(t)}cos(2\pi tT)]})
Here is the answer in the textbook:
However I got a different answer when working it out, and can't understand how they got to that result from the textbook.
Here is my working out:
