proof q (1 Viewer)

medaspirant · Jan 23, 2022

if any1 could assist me in this would be gr8ly appreciated

ExtremelyBoredUser · Jan 23, 2022

medaspirant said:
View attachment 34746
if any1 could assist me in this would be gr8ly appreciated

before I start, I think I've seen a variant of this question before, but I don't remember using contrapositive? But I think the same use of factorisation should work?

Contrapositive: n is not prime (composite) -> 2^n - 1 is not prime (composite)

If n is composite, there exists a set of integers $k,j$ such $n = kj$ as n is composite.

$2^{n} - 1 = 2^{kj} - 1$

Considering LHS

$2^{kj} - 1$

and I'm pretty sure you've seen this type of factorisation somewhere

$x^{n} - 1 = (x-1)(x^{n-1} + x^{n-2} .... + x +1)$

e.g (you've most likely seen this)
$x^{3} - 1 = (x-1)(x^{2} + x^{1} + x + 1)$
so pretty much the - 1 subtracts all the terms from x*x^{n-2} to x*{1} and you are left with x*x^{n-1} - 1 which is simply x^{n} - 1.

So letting x = 2^j and n = k

$2^{kj} - 1 = (2^j-1)((2j)^{k-1} + (2j)^{k-2} .... + 2j +1)$
$2^{kj} - 1 = (2^j-1)((2)^{(j)k-1} + (2)^{(j)k-2} .... + 2j +1)$

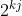
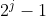
Hence clearly $2^{kj}$ divides $2^{j} - 1$ as from the equation, meaning that it has more factors than 1 and itself and therefore $2^{kj} - 1= 2^{n} - 1$ is not prime/composite.

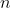
As the contrapositive is logically equivalent to the original statement, if $2^{n} - 1$ is prime then $n$ is prime.

Make a Difference – Donate to Bored of Studies!

proof q (1 Viewer)

medaspirant

Member

ExtremelyBoredUser

Bored Uni Student

Users Who Are Viewing This Thread (Users: 0, Guests: 1)