More SHM (1 Viewer)

HoldingOn · Jul 18, 2018

A particle is moving in SHM in a straight line. It’s max speed is 2m/s and it’s max acceleration is 6m/s^2. Find the amplitude and the period of the motion.

Also in $$v^2=n^2(a^2-(x-c)^2)$$ is $$ c$ always the centre of motion?

Thanks

fan96 · Jul 18, 2018

Starting with the acceleration equation:

$\ddot x = -n^2x$

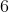
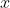
It is given that the maximum acceleration is $6$ , and from the equation we can see that the maximum acceleration occurs when $x$ is lowest.

i.e. $\ddot x_{\mathrm{max}} = -n^2\left(x_{\mathrm{min}}\right)$

Substituting in, we get 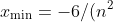$x_{\mathrm{min}} = -6/(n^2) \implies a = 6/(n^2)$ .

(This is only valid if we assume that the origin is the centre of motion, but this assumption can be made "without loss of generality" since the velocity and acceleration of an object under SHM are not dependent on its original position)

Then moving to the velocity equation:

$v^2 = n^2(a^2-x^2)$

It is given that $|v|_{\mathhm{max}} = 2 \implies -2 \leq v \leq 2$ .

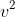
From the equation it is clear that $v^2$ is at a maximum when $x = 0$ .

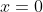
i.e. $\left(v_{\mathrm{max}}\right)^2 = n^2(a^2-0)$

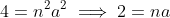
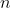
Therefore $4 = n^2a^2 \implies 2 = na$ , since $n$ and $a$ must both be positive.

Taking the two equations

$a = \frac{6}{n^2}$

$2 = na$

and solving gives $n=3,\,\,a = 2/3$ .

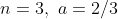
For your second question the answer is yes.

Make a Difference – Donate to Bored of Studies!

More SHM (1 Viewer)

HoldingOn

Active Member

fan96

617 pages

Users Who Are Viewing This Thread (Users: 0, Guests: 1)