Investigation of a certain function (1 Viewer)

Sy123 · Nov 23, 2014

So, just for fun I wanted to investigate the properties of this function:

$f(x) = \int_0^{\frac{\pi}{2}} \frac{\sin (xt)}{\sin t} \ $d$t , \ $and$ \ x \in \mathbb{R}$

Right now I know:

$\\ $Define$ \ I(N) = \int_0^{\frac{\pi}{2}} \frac{\sin ((2N)t)}{\sin t} \ $d$t , \ N \in \mathbb{N}$

$\\ $Define$ \ f(2N+1) = J(N) = \int_0^{\frac{\pi}{2}} \frac{\sin ((2N+1)t)}{\sin t} \ $d$t , \ N \in \mathbb{N}$

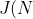$J(N) = \begin{cases}\frac{\pi}{2}, \ N \geq 0 \\ -\frac{\pi}{2}, \ N < 0 \end{cases}$

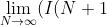$\\ \lim_{N \to \infty} (I(N+1) - I(N-1)) = \pi - 2$

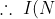$\\ \therefore \ I(N) \rightarrow \infty \ $as$ \ N \ $increases without bound$$

(I can provide proof if people are interested)

What else can we derive for this function (other than obvious things like f(x) = - f(-x))?

----

EDIT1:

If I did my differentiation right (please correct if I am wrong), then:

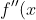$f''(x) + x^2 f(x) = 0$

And an elementary function cannot be derived from this (as expected)

FrankXie · Dec 2, 2014

Sy, that's not the correct way you differentiate an integral with an unknown in it (unless i am mistaken).

$f^\prime(x)=\int_0^{\frac{\pi}{2}}\frac{d}{dx} \left( \frac{\sin(xt)}{\sin{t}} \right)dt=-\int_0^{\frac{\pi}{2}}\frac{t\cos(xt)}{\sin{t}}dt$

$f^\prime(x)=\int_0^{\frac{\pi}{2}}\frac{t^2\sin(xt)}{\sin{t}}dt$

FrankXie · Dec 2, 2014

Here is a little thing I find out:

$f(x+2)-f(x)=\int_0^{\frac{\pi}{2}}\frac{\sin[(x+2)t]-\sin(xt)}{\sin{t}}dt=-\frac{2}{x+1}\sin\left(\frac{x+1}{2}\pi\right)$

From which some results may be derived?

Make a Difference – Donate to Bored of Studies!

Investigation of a certain function (1 Viewer)

Sy123

This too shall pass

FrankXie

Active Member

FrankXie

Active Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)