- Joined
- Feb 16, 2005
- Messages
- 8,397
- Gender
- Male
- HSC
- 2006
As a continuation of what I posted in the other thread. (I know someone just posted another one up but this is typed in LaTeX! Not written!  )
)
DISCLAIMER: I do not guarantee the correctness of these answers. If there is any error, let me know or post up the correction yourself.
Question 8a)
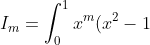^5\,dx\\\\u=x^{m-1}\Rightarrow du=(m-1)x^{m-2}\,dx\\\\dv=x(x^2-1)^5\,dx\Rightarrow v=\dfrac{(x^2-1)^6}{12}\\\\I_m=\left [ \dfrac{x^{m-1}(x^2-1)^6}{12} \right ]_0^1-\dfrac{m-1}{12}\displaystyle\int_0^1x^{m-2}(x^2-1)(x^2-1)^5\,dx\\\\I_m=-\dfrac{m-1}{12}\displaystyle\int_0^1[x^m(x^2-1)^5-x^{m-2}(x^2-1)^5]\,dx\\\\12I_m=(m-1)(I_{m-2}-I_m)\\\\\therefore I_m=\dfrac{m-1}{m+11}I_{m-2})
Question 8b)
i)

ii)
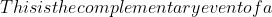 hence probability is $ 1 - \dfrac{7!}{7^7})
iii)
 hence we multiply by 6. Now consider possibilities where numbers other than 1 are not selected which leads to multiplication by 7. \\\\So probability is $\dfrac{\frac{7!}{2}\times 6\times 7}{7^7})
Question 8c)
i)
\\\\M \geq |a_{n-1}|\Rightarrow M|\beta|^{n-1}\geq |a_{n-1}\beta^{n-1}|\\\\M \geq |a_{n-2}|\Rightarrow M|\beta|^{n-2}\geq |a_{n-2}\beta^{n-2}|\\\\M \geq |a_{n-3}|\Rightarrow M|\beta|^{n-3}\geq |a_{n-3}\beta^{n-3}|\\\\...etc\\\\M \geq |a_0|\\\\$Addition of these inequalities $\\\\M(|\beta|^{n-1}+|\beta|^{n-2}+...+1)\geq |a_{n-1}\beta^{n-1}| + |a_{n-2}\beta^{n-2}| + ... + |a_0|\\\\$But from triangle inequality $\\\\|a_{n-1}\beta^{n-1}| + |a_{n-2}\beta^{n-2}| + ... + |a_0| \geq |a_{n-1}\beta^{n-1} + a_{n-2}\beta^{n-2} + ... + a_0|\\\\\Rightarrow M(|\beta|^{n-1}+|\beta|^{n-2}+...+1)\geq |a_{n-1}\beta^{n-1} + a_{n-2}\beta^{n-2} + ... + a_0|\\\\ $But $\beta$ is a root of $P(z)$ \\\\\Rightarrow \beta^n+a_{n-1}\beta^{n-1} + a_{n-2}\beta^{n-2} + ... + a_0 = 0\\\\\Rightarrow a_{n-1}\beta^{n-1} + a_{n-2}\beta^{n-2} + ... + a_0 = -\beta^n\\\\\therefore M(|\beta|^{n-1}+|\beta|^{n-2}+...+1)\geq |-\beta^n| = |\beta|^n)
ii) Courtesy of mma03 after realising my own solution had an error
(|\beta|^{n-1}+|\beta|^{n-2}+....+ |\beta| + 1)\\\\\Rightarrow M(|\beta|^{n-1}+|\beta|^{n-2}+...+1) \geq (|\beta| - 1)(|\beta|^{n-1}+|\beta|^{n-2}+....+ |\beta| + 1) + 1 \\\\> (|\beta| - 1)(|\beta|^{n-1}+|\beta|^{n-2}+....+ |\beta| + 1) \\\\\Rightarrow M > |\beta| - 1\\\\\therefore |\beta| < 1 + M)
An alternative, courtesy of largarithmic
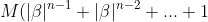 \geq |\beta|^n\\\\\Rightarrow M(|\beta|^{n-1}+|\beta|^{n-2}+...+1) + (|\beta|^{n-1}+|\beta|^{n-2}+...+1) \\\\\geq |\beta|^n+|\beta|^{n-1}+|\beta|^{n-2}+...+1\\\\\Rightarrow (M + 1)(|\beta|^{n-1}+|\beta|^{n-2}+...+1) \geq |\beta|^n+|\beta|^{n-1}+|\beta|^{n-2}+...+1 \\\\>|\beta|^n+|\beta|^{n-1}+|\beta|^{n-2}+...+|\beta|\\\\\Rightarrow (M + 1)(|\beta|^{n-1}+|\beta|^{n-2}+...+1) > |\beta| (|\beta|^{n-1}+|\beta|^{n-2}+...+1)\\\\\therefore |\beta| < M + 1)
Question 8d)
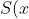=\displaystyle\sum_{k=0}^nc_k\left ( x+\dfrac{1}{x}\right )^k\\\\\\$Let $z=x+\dfrac{1}{x}$ where $x\in\mathbb{R}\\\\\Rightarrow S(x)\equiv s(z)=\displaystyle\sum_{k=0}^nc_kz^k=c_0+c_1z+c_2z^2+...+c_nz^n\\\\$Suppose that there exists a root $z=\beta$ such that $s(z)=0$ which is equivalent to solving $S(x)=0\\\\c_0+c_1\beta+c_2\beta^2+...+c_n\beta^n=0\\\\\Rightarrow \dfrac{c_0}{c_n}+\dfrac{c_1}{c_n}\beta+\dfrac{c_2}{c_n}\beta^2+...+\beta^n=0\\\\\Rightarrow P(\beta)=0 $ where $a_0=\dfrac{c_0}{c_n}, a_1=\dfrac{c_1}{c_n},..., a_{n-1}=\dfrac{c_{n-1}}{c_n}\\\\$Note that $|c_k|\leq |c_n| \Rightarrow \dfrac{|c_k|}{|c_n|}=|a_k|\leq 1 $ for all $k < n\\\\\Rightarrow M=\max(|a_{n-1}|,|a_{n-2}|,...,|a_0| )\leq 1\\\\\Rightarrow 1 + M \leq 2)
=0\\\\\Rightarrow x^2-\beta x + 1 = 0\\\\$Since we require $x\in\mathbb{R}$ then $\Delta\geq 0\\\\\Rightarrow \beta^2-4\geq 0\\\\\Rightarrow \beta \geq 2 $ or $ \beta \leq -2 \\\\\Rightarrow |\beta|\geq 2\\\\$This means that $\\\\|\beta|\geq 1 + M $ which contradicts the inequality in (c)(ii) which holds true for any $\beta$ which satisfies that polynomial, hence our assumption that a real root exists is false, thus $S(x)$ has no real solutions.$)
DISCLAIMER: I do not guarantee the correctness of these answers. If there is any error, let me know or post up the correction yourself.
Question 8a)
Question 8b)
i)
ii)
iii)
Question 8c)
i)
ii) Courtesy of mma03 after realising my own solution had an error
An alternative, courtesy of largarithmic
Question 8d)
Last edited:
