yeah true, i was introduced to this method in a number proof question: Prove that the second digit after the decimal point of √2 is 1 without a calculator.
and the working out started with this:
1.41 < √2 < 1.42
then it squared everything.
then it evaluated 1.41^2 and 1.42^2 and showed that the inequality was true.
is there an alternate method possible for this question?
but yeah some questions seem to just be unlocked with this method, kind of like reverse engineering the question
This method is valid as, for any positive reals,
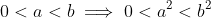
because
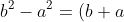(b - a) > 0 \implies b - a > 0)
.
It suffices as a method to establish that the decimal expansion begins
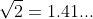
as the function
 = x^2 - 2)
is continuous throughout its domain and changes sign on the open interval
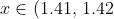)
, and so there must be at least one solution of
 = 0)
within that interval - and since there are only two solutions,
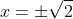
, it must be the positive value that satisfies
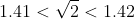
Note, however, that you would need to show that the root is within
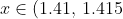)
to establish that
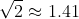
to three significant figures.
A method for finding roots called Newton's method would provide an alternative approach to this problem, but is no longer included in the MX1 or MX2 syllabi.
For example, starting with an initial approximation of
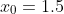
, the sequence of approximations
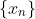
would be:
^2 - 2}{2\times\frac{3}{2}} = \frac{17}{12} = 1.416\ 666\ 666... \qquad \qquad \text{is correct to 2 decimal places} \\ \text{The third approximation} \qquad \qquad x_2 &= \frac{17}{12} - \cfrac{\left(\frac{17}{12}\right)^2 - 2}{2\times\frac{17}{12}} = \frac{577}{408} = 1.414\ 215\ 686... \qquad \qquad \text{is correct to 5 decimal places} \end{align*})
Starting from a better first approximation,
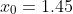
, the approximations converge to
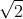
more rapidly:

... though I do admit that calculating the decimal form of some of these fractions isn't easy without a calculator!
Under the old syllabus, there was a final question on an MX2 paper (1988, if I recall correctly) that showed that using Newton's Method and starting from the first approximation
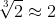
, the 12th approximation to
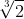
was correct to at least 267 decimal places.
